Экзамен по теории чисел II – вариант
shinymath, · Categories: Без рубрикиВариант для дистанционного участия. Правила и Гугл-форма — в посте ниже.
Faculty of Mathematics
Вариант для дистанционного участия. Правила и Гугл-форма — в посте ниже.
Итоговый экзамен по курсу Введение в теорию чисел состоится 15 июня с 16:20 до 19:20. За очное участие добавляется 2 балла к оценке за экзамен. У тех, кто пишет дистанционно, есть дополнительные полчаса (до 19:50) для того, чтобы отсканировать работу в один pdf файл и отправить через Гугл-форму. Во время экзамена можно пользоваться любыми неинтерактивными материалами. Если используете в решении теорему без доказательства, то приведите точную формулировку теоремы и ссылку на источник, где она доказывается.
Вариант появится в 16:20 отдельным постом выше. На полный балл достаточно решить любые 6 задач.
Гугл-форма для отправки контрольной (закроется в 19:50)
Комментарий для НЕ писавших контрольную: Если вы не писали контрольную, то вы можете написать её в рамках экзамена. Для этого нужно сдать решения нескольких задач (не более шести) через 80 минут после начала экзамена. Из оценок за эти задачи сформируется оценка за контрольную из расчёта 2 балла за задачу (плюс 2 балла за очное участие). При этом вы можете продолжить решать остальные задачи, чтобы учесть их (вместе с уже сданными) в оценке за экзамен из расчёта пять третей балла за задачу.
Обязательный экзамен для 4-курсников по курсу Введение в теорию чисел проходит 18 мая с 16:20 до 19:20. У тех, кто пишет дистанционно, есть дополнительные полчаса (до 19:50) для того, чтобы отсканировать работу в один pdf файл и отправить через Гугл-форму. Во время контрольной можно пользоваться любыми неинтерактивными материалами. Если используете в решении теорему без доказательства, то приведите точную формулировку теоремы и ссылку на источник, где она доказывается.
Вариант – задачи экзамена (на полный балл достаточно решить любые 6 задач)
Гугл-форма для отправки контрольной (закроется в 19:50)
Второй вариант контрольной по курсу Введение в теорию чисел проходит 6 апреля с 17:50 до 19:10. У тех, кто пишет дистанционно, есть дополнительные полчаса (до 19:40) для того, чтобы отсканировать работу в один pdf файл и отправить через Гугл-форму. Во время контрольной можно пользоваться любыми неинтерактивными материалами. Если используете в решении теорему без доказательства, то приведите точную формулировку теоремы и ссылку на источник, где она доказывается.
Вариант 2 – задачи контрольной (на полный балл достаточно решить любые 5 задач)
Гугл-форма для отправки контрольной (закроется в 19:40)
Первый вариант контрольной по курсу Введение в теорию чисел проходит 4 апреля с 11:30 до 12:50. У тех, кто пишет дистанционно, есть дополнительные полчаса (до 13:20) для того, чтобы отсканировать работу в один pdf файл и отправить через Гугл-форму. Во время контрольной можно пользоваться любыми неинтерактивными материалами. Если используете в решении теорему без доказательства, то приведите точную формулировку теоремы и ссылку на источник, где она доказывается.
Вариант 1 – задачи контрольной (на полный балл достаточно решить любые 5 задач)
Гугл-форма для отправки контрольной (закроется в 13:20)
On this webpage, you find information on courses and seminars that I teach. For the other information please see my official webpage.
Объявление: Выложены решения избранных задач экзамена.
Краткое описание: Цель курса – свободное владение основными понятиями алгебры и геометрии, такими как кольца, поля, группы преобразований, векторные пространства, линейные операторы. Курс является необходимым пререквизитом ко всем математическим курсам второго семестра.
Задачи для подготовки к экзамену.
Результаты (ссылка на Гугл-таблицу)
Темы для подготовки к коллоквиуму
Правила досрочного экзамена (1-й семестр)
Правила досрочного экзамена (2-й семестр)
Критерии оценки и статистика (письменный экзамен за 1-й семестр)
Оценка: Нельзя изучить математику, не решая задачи. Каждую неделю (в понедельник) на эту страницу будет выкладываться домашнее задание. Его нужно сдавать лектору в письменном виде (на задании указан срок сдачи).
В конце 1-го модуля состоится письменная контрольная, в конце 2-го модуля – письменный экзамен. В конце 3-го модуля состоится устный коллоквиум, в конце 4-го модуля – итоговый письменный экзамен. Также будет выдан листок с задачами повышенной сложности для устной сдачи.
За плагиат в любом виде ставится нулевая оценка за всю задачу, а при повторном плагиате – нулевая оценка за всё домашнее задание или контрольную. Плагиатом считается любое переписывание текста (из книги, чужой работы, Интернета и т.п.), автором которого вы не являетесь. Можно и нужно обсуждать задачи с другими студентами и преподавателями, читать книги и статьи, но записывать решения необходимо своими словами. Предоставление своего текста другому студенту для плагиата также считается плагиатом.
Итоговые оценки:
за 1 семестр 40% ДЗ + 20% К + 30% Э + 10% Л
за 2 семестр 30% ДЗ + 30% Кл + 30% Э + 10% Л
(округляется в большую сторону, например, 9.1 округляется до 10).
Учебники:
Дополнительное чтение:
Сдавать домашние задания нужно лектору в письменном виде. Задания, набранные в LaTeX, можно сдавать в электронном виде, присылая по адресу vkiritch at hse dot ru. Хотите научиться набирать в LaTeX? Читайте замечательный самоучитель (автор С.М.Львовский). Для лучшего усвоения сразу применяйте прочитанное к вёрстке домашних заданий.
Домашние задания проверяет учебный ассистент Рената Валиева rfvalieva at edu dot hse dot ru. Ей можно задать вопросы по проверке и оцениванию домашних заданий.
Модуль 4
Семинар 14 и ДЗ 7 (срок сдачи 17 апреля) – проекции
Семинар 15 – проективные пространства и аффинные карты
Семинар 16 и ДЗ 8 (срок сдачи 15 мая) – проективные преобразования и двойное отношение
Семинар 17 – проективная и полярная двойственность
Семинар 18 – преобразования Мёбиуса
ДЗ 9 – срок сдачи 22 мая
Листок 3 – срок сдачи 13 июня
Семинар 19 – евклидовы и гиперболические плоскости Гильберта
ДЗ 10 – срок сдачи 3 июня
Семинар 20 – сюрпризы гиперболической геометрии
Модуль 3
Семинар 1 – разбор задач экзамена
Семинар 2 – итерации линейных операторов
ДЗ 1 – срок сдачи 21 января
Листок 1 – срок сдачи 20 февраля.
Семинар 3 – собственные векторы и значения
Семинар 4 и ДЗ2 (срок сдачи 30 января) – след и характеристический многочлен
Семинар 5 и ДЗ3 (срок сдачи 6 февраля) – минимальный многочлен и корневые подпространства
Семинар 6 и ДЗ4 (срок сдачи 13 февраля) – жорданова нормальная форма и экспонента от оператора
Семинар 7 и ДЗ5 (срок сдачи 20 февраля) – абстрактные группы и их действия
Семинар 8 и ДЗ6 (срок сдачи 27 февраля) – факторгруппы
Семинар 9 (вместо ДЗ – подготовка к коллоквиуму) – двойственные пространства и сопряжённые операторы
Листок 2 – срок сдачи 17 апреля. Сдавать можно по предварительной договорённости Константину Панарину (kopanarin at yandex dot ru), Ильясу Байрамову (ibay@berkeley.edu) и Марку Алексееву (ubeta.1996@gmail.com). В последний день сдачи листка (17.04.2019) каждый студент может сдать не более трёх пунктов.
Семинар 10 – квадратичные формы в евклидовом пространстве
Семинар 11 – операторы в евклидовых и эрмитовых пространствах
Семинар 12 – сигнатура вещественных квадратичных форм
Семинар 13 – билинейные формы
Модуль 2
Листок 2 (срок сдачи 19 декабря) – листок нужно сдавать устно преподавателям по курсу на приёме задач и/или на присутственных часах. Также листок можно сдавать Ренате Валиевой и Константину Панарину kopanarin at yandex dot ru по предварительной договорённости. В последний день сдачи листка (19.12.2018) каждый студент может сдать не более трёх пунктов (суммарно из листков 2 и 3).
ДЗ6 и семинар 11 (срок сдачи ДЗ – 7 ноября) – векторное произведение, линейные операторы
Семинар 12 – линейные уравнения и ранги
ДЗ7 и семинар 13 (срок сдачи ДЗ – 12 ноября) – подпространства и ранги
ДЗ8 и семинар 14 (срок сдачи ДЗ – 19 ноября) – объёмы и определители
Семинар 15 – определители и матрицы
ДЗ9 и семинар 16 – аффинная геометрия
Семинар 17 – билинейные и квадратичные формы
Листок 3 (срок сдачи 19 декабря) – листок нужно сдавать устно преподавателям по курсу на приёме задач и/или на присутственных часах. Также листок можно сдавать Ренате Валиевой и Константину Панарину kopanarin at yandex dot ru по предварительной договорённости. В последний день сдачи листка (19.12.2018) каждый студент может сдать не более трёх пунктов (суммарно из листков 2 и 3).
ДЗ 10 и семинар 18 – евклидова геометрия
Семинар 19 – канонический вид квадратичных форм
Семинар 20 – задачи на максимум и минимум
Семинар 21 – ортонормальные базисы
Задачи для подготовки к экзамену
Модуль 1
ДЗ и семинар 1 (срок сдачи ДЗ – 17 сентября) – комплексные числа
Семинар 2 – линейные отображения
Семинар 3 – матрицы
ДЗ 2 (срок сдачи 24 сентября) – линейные отображения, матрицы, длины
Листок 1 (срок сдачи 15 октября) – листок нужно сдавать устно преподавателям по курсу на приёме задач и/или на присутственных часах. Также листок можно сдавать Ренате Валиевой и Константину Панарину kopanarin at yandex dot ru по предварительной договорённости. В последний день сдачи листка (15.10.2018) каждый студент может сдать не более трёх пунктов.
Семинар 4 – скалярное произведение, длины, углы
ДЗ 3 (срок сдачи 1 октября) – перестановки и группы симметрий
Семинар 5 – перестановки
Семинар 6 – симметрия
ДЗ4 и семинар 7 (срок сдачи ДЗ – 8 октября) – арифметика
Семинар 8 – гауссовы целые числа, многочлены, формальные степенные ряды
ДЗ5 и семинар 9 (срок сдачи ДЗ – 15 октября) – метод Гаусса
Семинар 10 – базисы
Задачи для подготовки к контрольной
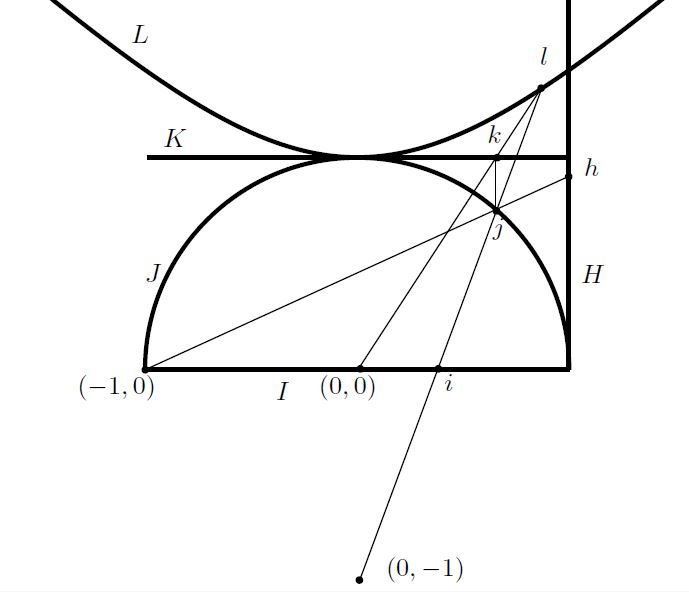
10.06.2019 Определения: пространство и метрика Минковского, конгруэнтные отрезки и углы в модели на гиперболоиде. Связь между движениями плоскости Лобачевского и преобразованиями Лоренца из специальной теории относительности. Пять моделей геометрии Лобачевского (на гиперболоиде, Клейна, на полусфере, Пуанкаре в диске и в верхней полуплоскости) и переходы между ними.
03.06.2019 Определения: прямые и точки, конгруэнтные отрезки и углы в модели Пуанкаре в круге и верхней полуплоскости. Физическая интерпретация модели Пуанкаре. Построение биссектрисы угла и восставление перпендикуляра в модели Клейна. Доказательство теоремы Брианшона через гиперболическую геометрию.
27.05.2019 Определения: прямые и точки, конгруэнтные отрезки и углы, расстояние в модели Клейна. Аддитивность дефекта треугольника. Если хотя бы один треугольник на плоскости имеет нулевой дефект, то и все треугольники имеют нулевой дефект. Связь между группой движений плоскости Лобачевского и проективными преобразованиями проективной плоскости.
20.05.2019 Определения: проективизация множества нулей однородного многочлена и проективное замыкание множества нулей неоднородного многочлена, рациональная параметризация коники. Примеры: проективизация конуса в R^3, проективное замыкание аффинной гиперболы, рациональная параметризация окружности. Связь с универсальной тригонометрической подстановкой и пифагоровыми тройками.
13.05.2019 Определения: окружности большого круга на сфере, равные сферические треугольники, дефект треугольника, угол параллельности. Площадь сферического треугольника пропорциональна его дефекту. Пятый постулат Евклида и эквивалентные ему утверждения (аксиомы Прокла-Плейфера, Валлиса, Лежандра и Льюиса Кэролла). Аксиома Лобачевского и гиперболическая геометрия. Модель Кэли-Клейна гиперболической геометрии.
29.04.2019 Определения: инверсия относительно окружности на евклидовой плосоксти, арбелос Архимеда. Связь инверсии и дробно-линейных преобразований комплексной прямой. Два взгляда на “школьную плоскость” как на аффинную карту (1) вещественной проективной плоскости и (2) комплексной проективной прямой. Полезные инструменты: (1) – проективные преобразования, двойное отношение, полярная двойственность, (2) – инверсии. Теорема о бабочке через проективные преобразования. Задача Паппа об арбелосе через инверсию.
22.04.2019 Определения: проективная двойственность, полярная двойственность относительно коники, полюс и поляра. Примеры: полярное преобразование плоскости относительно окружности, задача Штейнера о пяти кониках. Теоремы Паскаля и Брианшона как двойственные утверждения.
15.04.2019 Определения: проективные преобразования, дробно-линейные преобразование, двойное отношение, полный четырёхсторонник. Примеры: дробно-линейные преобразования прямой, инварианты четвёрки прямых на векторной плоскости. Проективное преобразование n-мерного проективного пространства определяется образами n+2 точек, никакие n+1 из которых не лежат в одной гиперплоскости. Теорема Мёбиуса-фон Штаудта (без доказательства).
08.04.2019 Определения: проективизация векторного пространства, проективные пространства и подпространства, однородные координаты, аффинные карты, аксиомы абстрактной проективной плоскости. Примеры: законы перспективы, вещественная и комплексная проективная прямая, проективная плоскость, игра Доббль, задача Эйлера о 36-ти офицерах. Две различные прямые на проективной плоскости всегда пересекаются в одной точке. Теорема Паппа.
18.03.2019 Определения: сигнатура квадратичной формы, положительный и отрицательный индексы инерции. Критерий Сильвестра положительной и отрицательной определённости квадратичной формы. Приложения в анализе (экстремумы функции нескольких переменных). Приложения самосопряжённых операторов в физике (бра и кет формализм).
11.03.2019 Определения: полуторалинейные и эрмитовы формы, эрмитово (унитарное) пространство, самосопряжённый оператор в эрмитовом пространстве. Примеры: квадрат модуля комплексного числа. Самосопряжённый оператор в эрмитовом пространстве диагонализуется в ортонормальном базисе. Собственные значения эрмитова оператора вещественны.
04.03.2019 Определения: квадратичные формы, квадрики, поляризация квадратичной формы, самосопряжённый оператор, связанный с квадратичной формой в евклидовом пространстве. Примеры: коники. Матрица квадратичной формы и матрица соответствующего ей самосопряжённого оператора совпадают в ортонормированном базисе. Квадратичная форма в евклидовом пространстве приводится к главным осям
25.02.2019 Определения: двойственное пространство, сложение линейных функций, векторы и ковекторы, сопряжённый оператор, двойственный базис, аннулятор подпространства. Примеры: базисы в пространстве многочленов и двойственные базисы (формулы Лагранжа и Тейлора), самодвойственность пространства квадратных матриц. Каноническое соответствие между подпространствами в V и подпространствами в V*. Канонический изоморфизм между V и V**. Размерности V и V* совпадают в конечномерном случае. Транспонированная матрица оператора совпадает с матрицей двойственного оператора в двойственном базисе. Билинейная форма как способ задать изоморфизм между V и V*.
18.02.2019 Определения: левые и правые классы смежности, нормальная подгруппа, факторгруппа, ядро и образ гомоморфизма. Примеры: группа Z/nZ вычетов по модулю n. Стабилизаторы точек в одной орбите сопряжены. Теорема Лагранжа. Группа простого порядка не содержит нетривиальных подгрупп. Нормальная подгруппа представляется как ядро гомоморфизма.
11.02.2019 Определения: группа, подгруппа, порядок группы, гомоморфизм, изоморфизм, действие группы на множестве, орбиты и стабилизаторы. Примеры: группа перестановок, GL(n), Z, Q, R, R^*, циклическая группа, группа диэдра. Порядок конечной группы равен произведению порядка орбиты на порядок стабилизатора.
04.02.2019 Определения: спектр оператора, инвариантные подпространства, прямая сумма подпространств. Пространство с оператором раскладывается в прямую сумму корневых подпространств. Жорданова нормальная форма нильпотентного оператора.
28.01.2019 Определения: жорданова клетка, минимальный многочлен оператора, собственные и корневые подпространства. У каждого оператора над полем комплексных чисел есть жорданова нормальная форма. Явные формулы для рекуррентных последовательностей.
21.01.2019 Определения: диагонализуемые операторы, след оператора, сопряжённые (подобные) матрицы. Матрицы оператора в разных базисах сопряжены. Почти любой оператор над полем комплексных чисел диагонализуем. Теорема Гамильтона-Кэли. Вычисление степени оператора с помощью интерполяционного многочлена Лагранжа.
14.01.2019 Определения: собственные векторы, собственные значения и характеристический многочлен оператора. Связь с физическими задачами и линейными дифференциальными уравнениями. Собственные векторы с попарно различными собственными значениями линейно независимы.
Примерный план лекций (курсивом отмечены темы, которые будут изучаться, если останется время):
1-й семестр
17.12.2018 Определения: построение циркулем и линейкой, построимые комплексные числа, расширения полей, поликвадратичные расширения, степень расширения. Примеры: классические задачи древности, построение правильного пятиугольника. Степень башни расширений полей. Доказательство неразрешимости задач об удвоении куба и трисекции угла.
10.12.2018 Определения: изометрии (движения) евклидова пространства, группы GL_n(R) (полная линейная), SL_n(R) (специальная линейная), O_n(R) (ортогональная), SO_n(R) (специальная ортогональная). Примеры: группа O_2(R), группа поворотов плоскости SO_2(R), группа поворотов трёхмерного пространства SO_3(R). Изометрия является линейным преобразованием. Классификация движений плоскости.
03.12.2018 Определения: матрица Грама билинейной формы. Примеры: матрица Грама стандартного скалярного произведения. Ортогонализация Грама-Шмидта для положительно определённой симметричной билинейной формы. Квадрат объёма параллелепипеда как определитель матрицы Грама. Неравенство Коши-Буняковского-Шварца. Формула для расстояния от вектора до подпространства через матрицы Грама. Разложение вектора по ортонормальному базису. Метод наименьших квадратов.
26.11.2018 Определения: евклидовы пространства, длины, углы, расстояния, ортогональное дополнение к подпространству, ортогональный и ортонормированный базисы. Примеры: школьная плоскость, физическое пространство. Теорема Пифагора. Неравенство треугольника. Расстояние от точки до подпространства, угол между вектором и подпространством, расстояние между скрещивающимися подпространствами.
19.11.2018 Определения: аксиоматическое определение определителя (полилинейность, кососимметричность, нормировка), алгебра Грассмана; аффинные пространства и подпространства, репер. Примеры: векторное произведение как внешнее; пространство решений неоднородной системы линейных уравнений. Теорема существования и единственности определителя. Разложение определителя по строке. Определитель произведения матриц равен произведению определителей. Связь понятия репера и понятия базиса.
12.11.2018 Определения: определитель как ориентированный объём параллелепипеда, определитель линейного оператора, определитель матрицы. Примеры: определители в размерности 2 и 3, равносоставленные параллелограммы имеют равные площади. Вычисление определителя с помощью элементарных преобразований столбцов. Явная формула для определителя.
29.10.2018 Определения: матрица линейного оператора, ранг линейного оператора и матрицы. Примеры: движения плоскости, преобразования фоторедактора, дифференцирование многочленов, линейные функции. Как выбрать базисы в области определения и области значений, чтобы матрица линейного оператора имела наиболее простой вид. При композиции линейных операторов их матрицы перемножаются. Ранг оператора равен размерности его области определения минус размерность ядра. Критерии обратимости линейного оператора в терминах его ядра и образа.
15.10.2018 Определения: векторное подпространство, пересечение и сумма подпространств, порождающий набор, базис, координаты, размерность, линейный оператор, его ядро и образ, изоморфизм. Примеры: базисы в пространстве многочленов и интерполяционная формула Лагранжа. Любые два базиса в векторном пространстве равномощны. Каждое векторное пространство изоморфно координатному векторному пространству.
8.10.2018 Определения: векторное пространство, векторы, скаляры, линейная комбинация, линейная зависимость, элементарные преобразования строк матрицы. Примеры: координатное векторное пространство. Метод Гаусса. Приведение матрицы к стандартной ступенчатой форме преобразованиями строк, решение систем линейных уравнений и поиск линейной зависимости между векторами.
1.10.2018 Определения: делимость в кольцах, простые и неприводимые элементы, деление с остатком. Примеры: целые числа, гауссовы целые числа, неприводимый и не простой элемент в Z[\sqrt 5], кольцо многочленов с коэффициентами в поле. Решето Эратосфена. Алгоритм Евклида, цепные дроби и представление НОД(a,b) в виде линейной комбинации чисел a и b. Основная теорема арифметики. Деление с остатком в гауссовых целых числах.
24.09.2018 Определения: группа перестановок, инверсии (беспорядки), длина и знак перестановки, транспозиции и циклы. Связь между знаком перестановки и ориентированным объёмом параллелепипеда. Перестановка раскладывается в произведение непересекающихся циклов. Задача об арестантах.
17.09.2018 Определения: скалярное произведение, длина, расстояние, метрика, площадь, объём. Примеры: евклидова метрика, метрика такси. Билинейность скалярного произведения. Вычисление косинуса угла между векторами через скалярное произведение. Вычисление площади параллелограмма через равносоставленность.
10.09.2018 Определения: сложение векторов и умножение на число в вещественном координатном пространстве, 8 свойств (“аксиомы векторного пространства”), линейное отображение, матрицы и произведение матриц. Примеры: одномерный случай, матрица умноженная на столбец дает столбец, матрица для поворота на 90 градусов и для поворота на произвольный угол. Каждое линейное отображение задается матрицей.
06.09.2018 Определения: кольцо, поле. Примеры: целые числа, комплексные числа, поле из двух элементов. Почему (-1)(-1)=1. Комплексные числа как преобразования плоскости. Основная теорема алгебры.
Grigory Yurgin: Complete classification of n-dimentional lattice polytopes of degree 1
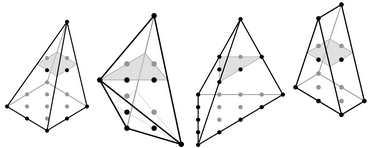
Let P be an n-dimensional lattice polytope. Recall that P has degree 1 iff it is not a standard simplex and kP has no interior lattice points for k = 1, 2, …, n-1. In this talk we shell obtain the complete classification of n-dimensional polytopes of degree 1. We are going to use combinatorial methods only.
Next Wednesday we have no talks, and this Wednesday we shall see two points of view towards the important phenomenon of hollow polytopes: lattice polytopes whose interior avoids the lattice.
17:00 Vjacheslav Zhukov: Maximal lattice-free polyhedra: finiteness and an explicit description in dimension three
We shall study lattice poyhedra whose interior avoids a given
sublattice. The number of maximal (by inclusion) polyhedra of this type
is finite modulo authomorphisms of the lattice. We shall prove this fact
and see how to classify such polyhedra in dimension
3.
18:30 Evgeniy Pavlov: Hollow Convex Polytopes
This is the second talk in a series of lectures devoted to the study of
convex bodies and polyhedra without interior lattice points. In this
part we combine the results of Kannan, Lovasz and Pikhurko to show that
every hollow lattice d-polytope either admits
a projection onto a hollow lattice (d-1)-polytope, or belongs to one of
finitely many exceptions.
17:00 Yuri Rud’ko: The number of lattice polytopes of a given volume
We will study the following question: what is the number of different lattice convex polytopes of a given volume A in R^d. This question is rather well-studied. There are a few results of Arnold; Konyagin and Sevostyanov; Andrews and so on. I am going to tell about the best possible estimate (by Vershik and Barany) for the order of this number. It is rather close to the previously discussed Arnold’s result for the number of plane convex lattice polytopes but uses new methods to go through in higher dimentions.
18:30 Alexander Iuran: Covering minima and lattice-point-free convex bodies This is the first in a series of talks devoted to the study of convex bodies and polyhedra without interior lattice points. The topic originates from Minkowski’s “gometry of numbers’ and relates many fields in mathematics and its applicationss from number theory to optimization.
We will prove several inequalities about “covering minima” of a convex body, quantities which describe the ability of its integer translations to cover all the space. This allows to give bounds of O(dim^2) on the width of a convex body without lattice points. Even though the volume of such a body is unbounded, we will prove that it has a projection whose volume is not much greater than the determinant of the lattice.